The Mathematics of Lasca
Because Lasca has a pleasingly simple set of rules, and a symmetrical board, it lends itself to mathematical analysis. This page describes some mathematical facts and conjectures about Lasca.
The law of entropy
The number of pieces on the board either stays the same, or decreases, during the course of the game. This is quite obvious since a capture of a column leaves the number of pieces the same, but the capture of a single counter reduces the number of pieces by one.
It is perfectly possible for all the counters to end up in two columns at the end of the game.
Largest change in fortunes
What is the largest change in the number of pieces that can occur in a single move?
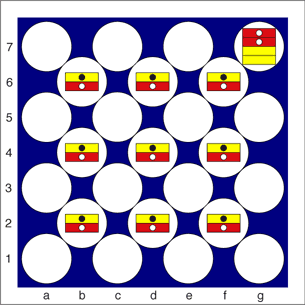
I believe the following example is the best solution to this. Black starts with one piece against White's nine, and it's Black to move:
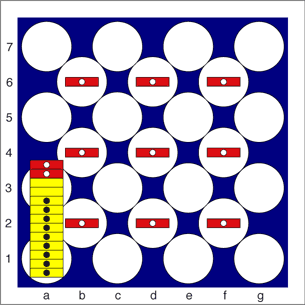
Black plays: g7xe5c6xa5xc3xe1xg3xe5xc3xa1, which is permitted because no piece is captured more than once, and the position is now:
Black now has ten pieces against White's none, a change of 18 pieces in Black's favour!
Alternating colours
It is fairly obvious that columns can either be white/black or black/white, but never alternating colours such as black/white/black or white/black/white:
The reason is that a piece can only append counters of the opposite colour under it. For an alternation like WBW to occur a white piece would have had to capture a white counter, which is impossible.
In mathematical notation, every Lasca column must have the form:
m x [wW], n x [bB] or m x [bB], n x [wW], where m is between 1 and 11 and n is between 0 and 11.
Here [wW] means either a white soldier or officer, and [bB] means either a black soldier or officer.
Impossible columns
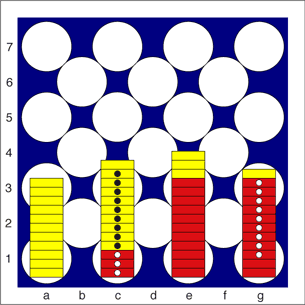
Because pieces of one colour can only get aggregated into columns by first being captured by the other player, Sprague and Cauer have been able to prove that the following types of column are impossible[1]:
11 x [wW], n x [bB] where n is between 0 and 11 (eg a1 below).
In other words, all the White pieces cannot end up in a single column, since to do so Black would first have to capture them all, in which case Black would have won before they can get liberated.
w, 9 x [wW], n x [bB] where n is between 3 and 11 (eg c1 below).
n x [wW], 11 x b where n is between 3 and 11 (eg e1 below).
w, n x [wW], 9 x [bB], 2 x b where n is between 0 and 9 (eg g1 below).
Proving these last three results is more complicated.
Examples of these four types of impossible column are shown in the following illustration:
- ^ Quelle: Ahrens, Altes und Neues aus der Unterhaltungs-mathematik, p. 164–167.